728x90
반응형
알고리즘을 처음 공부할 때, 많은 사람들이 어려워하는 개념이 바로 "동적계획법(DP)"입니다. 이 글에서는 DP를 어떻게 접근하고, 어떤 기준으로 적용할지 명확히 이해할 수 있도록 안내하겠습니다.
📌 동적계획법(DP)이 어려운 이유
DP는 문제를 작은 문제로 나누고, 그 결과를 활용하여 큰 문제를 해결하는 방식입니다. 하지만 처음부터 DP가 적용된다는 것을 떠올리기 쉽지 않죠. 문제를 보면 막막하게 느껴지기 때문입니다.
📌 DP를 명확히 적용하는 3가지 기준
다음의 기준을 보고 DP 적용 여부를 쉽게 판단해보세요.
- 반복되는 부분 문제가 있는가?
- 배수, 비율 등 간단한 규칙으로 최적이 가능한가? (그리디로 해결 가능)
- 작은 문제의 해답을 큰 문제에서 활용할 수 있는가? (점화식 판단)
이 기준을 충족하면 DP로 접근할 가능성이 높습니다.
📌 예시 문제: 동전 거스름돈
"1원, 4원, 5원짜리 동전으로 8원을 최소 개수의 동전으로 만드는 문제"
이 문제를 DP로 푸는 이유는 다음과 같습니다.
- 작은 문제(1원, 2원, ...)의 답을 반복해서 사용
- "1원 추가"라는 행동이 작은 문제와 큰 문제를 연결
📌 DP 풀이 과정 (Step by Step)
- 작은 문제부터 나누기
- 1원부터 목표금액까지 작은 문제로 나눈다.
- 점화식 설정
- 중복이 많이 되는 부분이 있는데 이 부분을 DP를 이용할 것입니다.
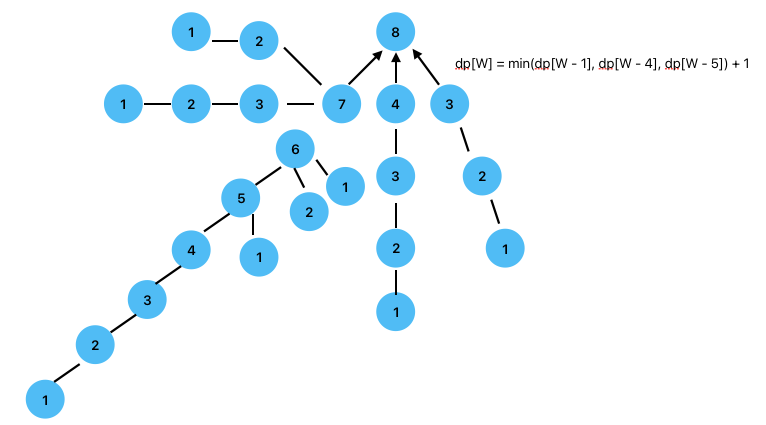
- 반복문이 가능하게 하는 점화식:
$$ dp[W] = min(dp[W - 1], dp[W - 4], dp[W - 5]) + 1 $$
3. 초기값 설정
- dp[0] = 0, 나머지 INF(불가능)
4. DP 테이블 채우기
| W | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| dp[W] | 0 | 1 | 2 | 3 | 1 | 1 | 2 | 3 | 2 |
| 1 | - | 1 | 2 | 3 | 4 | 2 | 2 | 3 | 4 |
| 4 | - | - | - | - | 1 | 2 | 3 | 4 | 2 |
| 5 | - | - | - | - | - | 1 | 2 | 3 | 4 |
- 예시로 W=8 계산:
- dp[8] = min(dp[7]+1=4, dp[4]+1=2, dp[3]+1=4) → 2 (4원짜리 2개)
- 계산 상세
- dp[0]=0
- dp[1]=dp[0]+1=1
- dp[2]=dp[1]+1=2
- dp[3]=dp[2]+1=3
- dp[4]=min(dp[3]+1, dp[0]+1)=min(4,1)=1
- dp[5]=min(dp[4]+1, dp[1]+1, dp[0]+1)=min(2,2,1)=1
- dp[6]=min(dp[5]+1, dp[2]+1, dp[1]+1)=min(2,3,2)=2
- dp[7]=min(dp[6]+1, dp[3]+1, dp[2]+1)=min(3,4,3)=3
- dp[8]=min(dp[7]+1, dp[4]+1, dp[3]+1)=min(3,2,4)=2
📌 DP 소스 코드(Java 예시)
int[] coins = {1, 4, 5};
int target = 8;
int[] dp = new int[target + 1];
for (int i = 1; i <= target; i++) {
dp[i] = Integer.MAX_VALUE;
}
dp[0] = 0;
for (int w = 1; w <= target; w++) {
for (int coin : coins) {
if (w - coin >= 0 && dp[w - coin] != Integer.MAX_VALUE) {
dp[w] = Math.min(dp[w], dp[w - coin] + 1);
}
}
}
System.out.println(dp[target]); // 결과 출력📌 하향식 vs 상향식 비교
- 하향식(재귀+메모이제이션): 큰 문제 → 작은 문제 (직관적)
- 상향식(반복문): 작은 문제 → 큰 문제 (효율적, 빠름)
코딩테스트에서는 상향식을 권장합니다.
📌 DP와 백트래킹의 관계
- 백트래킹은 모든 경우를 시도하며, 실패하는 분기를 빠르게 잘라냅니다.
- DP는 백트래킹 중 이미 계산한 상태를 저장하고 재사용합니다.
- DP는 백트래킹의 가지치기를 더욱 효율적으로 만들어줍니다.
📌 최종 정리 (의사결정 흐름)
"문제 발견 → 반복구조 체크 → 그리디 판단 → DP 판단(점화식 가능 여부) → 안되면 백트래킹 또는 완전탐색"
이 흐름대로 접근하면 문제를 빠르고 효율적으로 풀 수 있습니다.
📌 마무리: DP 사고력을 높이는 연습법
- DP는 결국 "기억의 기술"입니다. 한번 계산한 것을 반드시 기록하고, 다시 계산하지 않게 합니다.
- 문제를 분할할 수 있는 "점화식"을 빠르게 찾는 능력이 핵심입니다.
- 익숙해지면 문제를 보는 순간 DP인지 판단할 수 있게 됩니다. 꾸준히 연습하세요.
- 계단 오르기 문제, 거스름돈 문제를 자주 풀어보기
- 점화식 만드는 연습을 많이 해보기
- 작은 문제의 답을 기록(메모이제이션)하고 활용하는 습관 가지기
DP는 어려워 보이지만, 올바른 접근법과 연습을 통해 충분히 마스터할 수 있습니다. 이 글을 통해 DP의 개념을 명확하게 이해하고 자신감을 얻으시길 바랍니다!
참조
728x90
반응형
'CS > 알고리즘 & 자료구조' 카테고리의 다른 글
| [알고리즘] DFS(Depth-First Search, 깊이 우선 탐색) 문제 풀이 가이드 (2) | 2025.07.14 |
|---|---|
| [알고리즘] 슬라이딩 윈도우 풀이 가이드 (0) | 2025.07.14 |
| [수학적 처리] 증명된 수식을 로직으로 (1) | 2025.06.27 |
| [백준] BOJ 1874 스택 수열 (1) | 2025.06.09 |
| [백준] 숫자 카드 2 (0) | 2025.06.09 |